Matemáticas y epidemias
Héctor Ochoa Díaz López, Roberto Solís Hernández, José Ocampo López
Escalera y César Irecta Nájera
Cómo se propagan las
enfermedades infecciosas y cómo se les puede detener son cuestiones
fundamentales para la dupla del momento: matemáticas y epidemiología. A través
de sus modelos y métodos, estas disciplinas se combinan para brindar
información respecto al comportamiento de un virus y con ello actuar en
consecuencia.
“Las matemáticas salvan vidas”, aseguran Clara Grima, doctora en
matemáticas, y Enrique Borja, doctor en física, en Las matemáticas vigilan
tu salud. Modelos sobre epidemias y vacunas (Next Door
Publishers, 2017). Estos divulgadores de ciencia
explican la utilidad de dicha disciplina para entender cómo se propagan las enfermedades
infecciosas y cómo se les puede detener, ya que su diseminación se liga a leyes
matemáticas.
Las aplicaciones del saber matemático en la medicina, la epidemiología y la
salud pública, son un soporte de las acciones para entender las causas de los
padecimientos, determinar su distribución en la población, predecir su
evolución, desarrollar y evaluar medidas y estrategias para su control. Esto es
claro en los tiempos actuales, cuando la enfermedad covid-19 ocupa nuestras
vidas y las de muchos epidemiólogos que se dedican a estudiarla y combatirla.
El hecho de que las matemáticas sean tan importantes en varias áreas de las
ciencias biológicas, como la “epidemiología matemática”, surge de un enfoque
multidisciplinario que ha requerido modelos matemáticos como herramienta
conceptual; es algo parecido a usar un nuevo tipo de microscopio con el que se
pueden describir, explicar y, en ocasiones, anticipar comportamientos
específicos. En el presente artículo revisaremos brevemente ciertos aportes al
respecto, ejemplificando la aplicación de estos modelos a la actual
pandemia.
Las epidemias y algo de historia
Las epidemias son brotes regionales de una enfermedad con una propagación
intensa e inesperada (se vuelven pandemias al alcanzar una escala mundial).
Existen desde los inicios de la humanidad y han causado severos daños. La
historia europea registra las pestes Antonina, de Cipriano y de Justiniano en
los siglos II, III y VI, respectivamente, y por supuesto, la peste bubónica
(peste negra) proveniente de Asia, cuyas diferentes olas en el siglo XIV
acabaron con más de un tercio de la población de Europa en solo cinco años; fue
recurrente durante los siguiente tres siglos con grandes brotes en ciudades
como Londres, Roma, Hamburgo y Colonia. En América podemos mencionar la
viruela, tifoidea, malaria y fiebre amarilla, así como las letales
epidemias del siglo XX: la influenza española, que mató a más de 50 millones de
personas, y el sida, que causó 30 millones de defunciones.
En las dos primeras décadas del siglo XXI, el mundo también ha presenciado
grandes epidemias: en 2002-2003, el síndrome agudo respiratorio (SARS); en 2009,
la influenza H1N1; en 2012, el síndrome respiratorio de Oriente Medio (MERS);
en 2014, el ébola, y a fines de diciembre de 2019, el SARS-CoV-2, que se
propagó desde Wuhan, Hubei, China, a más de 200 países, para ser el
responsable de más de un millón de muertes y 40 millones de casos en el mundo
(octubre de 2020). Todo esto ha renovado el interés por la aplicación de las
matemáticas en el estudio de las epidemias, dado que favorecen su control.
Precursores de la
epidemiología matemática
La
epidemiología es el estudio de la distribución y los determinantes de las
enfermedades, eventos y estados de salud en la población, y la aplicación de
este estudio al control sanitario. La epidemiología matemática utiliza modelos para
analizar la dinámica de las enfermedades infecciosas y el efecto de las medidas
de mitigación. Por sus aportes, podemos mencionar a varios precursores de estas
disciplinas, comenzando por John Graunt, estadístico y demógrafo
inglés (1620-1674), quien estudió los registros semanales de las causas de
muerte en las parroquias de Londres, y comparó el riesgo de morir por
diferentes enfermedades en su libro Natural and Political
Observations Made upon the Bills
of Mortality (1662). Un contemporáneo suyo,
William Petty, filósofo, médico, economista y estadístico inglés (1623-1687),
publicó sus estudios de los patrones de natalidad y mortalidad, y propuso, por
vez primera, la creación de una agencia gubernamental para la recolección e
interpretación de los nacimientos, casamientos y muertes.
El primer modelo en epidemiología matemática se atribuye a Daniel
Bernoulli, un matemático, físico y médico holandés (1700-1782) que demostró
que la esperanza de vida aumentaba eliminando la viruela mediante la
variolización (inoculación de la viruela, procedimiento anterior a la invención
de la vacuna).(1)
Por su parte, John Snow, anestesiólogo inglés y médico de la reina Victoria
(1813-1858), contribuyó a entender el mecanismo de transmisión de las
enfermedades infecciosas, incluso antes de que se conocieran los agentes
infecciosos, al reconocer el patrón temporo-espacial
de la propagación del cólera en Londres, Inglaterra. A William Farr, estadístico y epidemiólogo inglés (1807-1883),
pionero en la recolección y análisis de estadísticas de morbi-mortalidad,
se le atribuye la descripción del comienzo, pico y declinación de una epidemia con
una curva en forma de campana (Campana de Farr).
Otros médicos y científicos que hicieron grandes contribuciones a la
epidemiología fueron Louis Pasteur (1822-1875), Robert Koch (1843-1910) y
Joseph Lister (1827-1912), quienes concibieron la teoría germinal de las
enfermedades infecciosas. Finalmente, ya en el siglo XX, resultó esencial el
aporte de los modelos epidémicos compartimentales (2) que desarrollaron, entre
1900 y 1935, Ronald Ross, W. H. Hamer, W. O. Kermack
y A. G. McKendrick, médicos en salud pública. El
trabajo de Ross respecto a la dinámica de la transmisión de la malaria introdujo
el concepto del número básico de reproducción o R0.
Número básico de reproducción: R0
El R0 o número básico reproductivo es un parámetro útil
en la caracterización de las epidemias. Mide la velocidad con la que se propaga
una infección y su potencial pandémico. Se refiere al número promedio de personas
infectadas por un individuo, y se incluyen todos los casos secundarios
afectados por uno primario. Es muy útil para determinar la proporción de la
población que debe vacunarse a fin de evitar que una epidemia se propague. Si
una enfermedad nueva entra en una población, ¿cuál es la probabilidad de que se
extienda? La respuesta la da el parámetro R0:
R0 < 1: la enfermedad desaparece
R0 = 1: la enfermedad se vuelve endémica
R0 > 1: habrá una epidemia
La covid-19 tiene un R0 de 2.68, lo que confirma su
facilidad de expansión.
El modelo SIR
El avance de las matemáticas en cuanto a su diversidad y complejidad ha
dado lugar a gran cantidad de subespecialidades que permiten abordar los
problemas planteados por la epidemiología desde diferentes enfoques. Es el caso
de las proyecciones que realiza y difunde el gobierno federal acerca de la
evolución de la covid-19 en México; se basan en el modelo matemático AMA, que
es compartimental. Su punto de partida es el modelo SIR, el cual es muy
ilustrativo y lo describiremos para comprender los fundamentos del AMA. El SIR puntualiza
qué porcentaje de una población se encuentra en una de tres categorías relacionadas
con una epidemia a lo largo del tiempo:
- Susceptibles (S), agrupa
a quienes no han estado en contacto con la enfermedad y pueden contraerla.
- Infecciosos (I), los que
enfermaron y todavía son foco de contagio.
- Recuperados (R), todos aquellos
que contrajeron el padecimiento, pero ya no lo transmiten por haberse
recuperado y ser inmunes, o por haber fallecido.
Las reglas que rigen la dinámica de estas clasificaciones se esquematizan
en la figura 1: las personas de la categoría S pasarán a la I a
un ritmo definido por la tasa de transmisión k1; mientras que las de la
categoría I pasan a la R a un ritmo dado por la tasa de
recuperación k2. Si estas reglas se traducen en ecuaciones diferenciales y se
resuelven, se obtienen resultados como los de la figura 2. En la curva punteada
se observa que la fracción de personas infectadas aumentará gradualmente hasta
llegar a un punto máximo, al que se conoce como acmé, y después disminuirá poco
a poco hasta que todos estén en la categoría de recuperados. Es un modelo
muy ilustrativo de brotes epidémicos del pasado, como la influenza española de
1918.

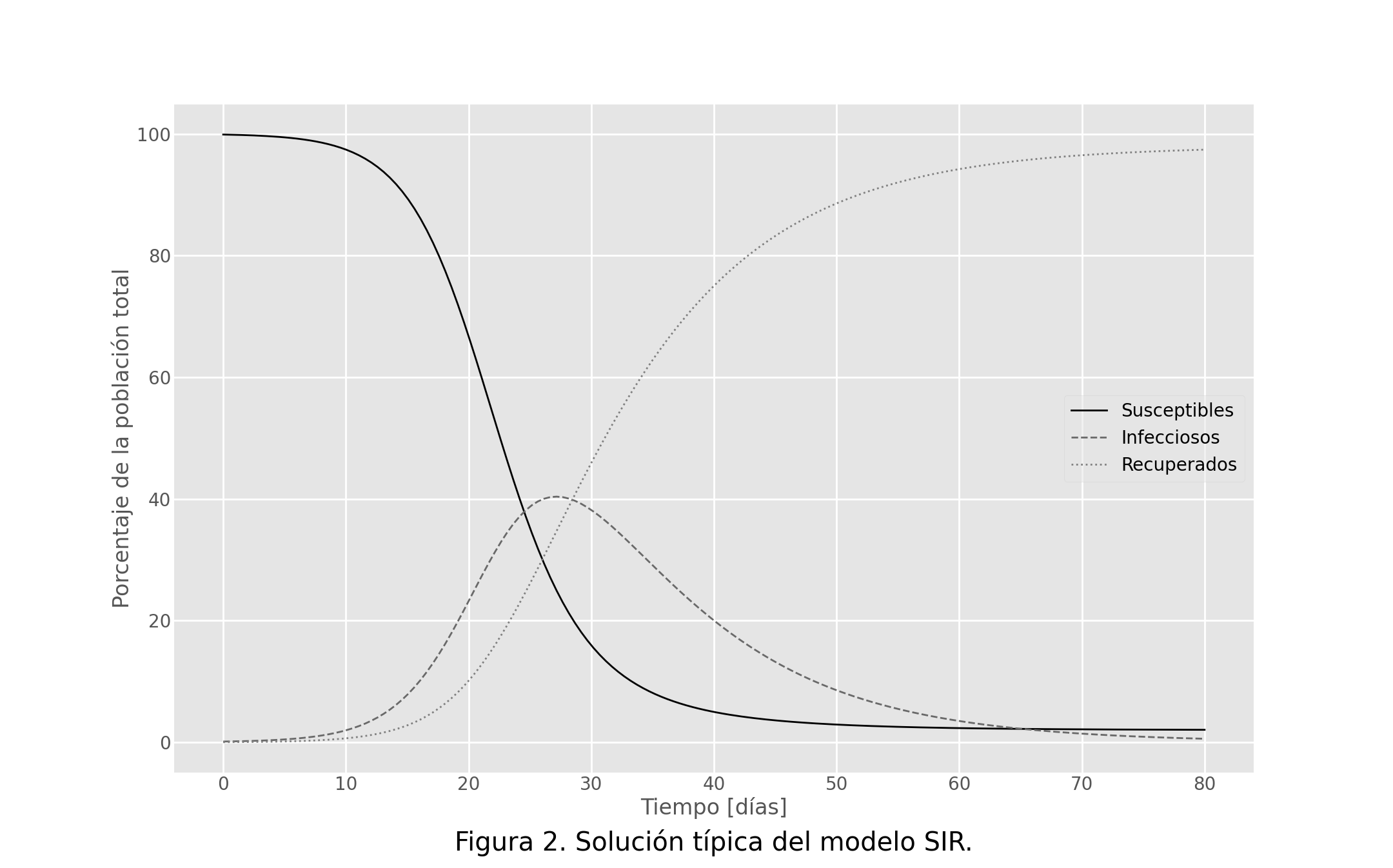
Figura 1. Diagrama de flujo del modelo SIR
Además del SIR, existen otros modelos compartimentales clásicos que
modifican las categorías y sus reglas de interacción para incluir características
de diferentes tipos de epidemias. Por ejemplo, los modelos SEIR se aplican en
enfermedades con periodos prolongados de incubación, como la varicela y el
dengue, e incluyen la categoría “expuestos” (E), que agrupa a individuos
infectados, pero que en periodo de incubación aún no pueden contagiar a otros.
También están los modelos SIS, donde las personas pasan de susceptibles a infecciosas
para luego regresar a susceptibles, como sucede en gran parte de las
enfermedades de transmisión sexual (ETS), ya que solo algunas dejan inmunidad.
Herramientas computacionales en las prácticas modernas
Con la covid-19 están en auge los modelos matemáticos o simulaciones
computacionales que ayudan a entender la compleja naturaleza y dinámica de la pandemia.
Pese a que diariamente se genera una cantidad colosal de registros de datos, el
abanico de posibilidades para el análisis y modelado epidemiológico-matemático
es más amplio y robusto que en cualquier otro momento de la historia. Las
herramientas computacionales cobran un rol destacado porque facilitan la
aplicación de algoritmos y de nuevas metodologías, por ejemplo, el big data, el aprendizaje automático y las redes
neuronales mediante sistemas de inteligencia artificial. Sin embargo, los
modelos matemáticos solo son representaciones de la realidad, con incertidumbre
y gran dependencia de datos de buena calidad; si estos son inconsistentes o
poco fiables, las predicciones o estimaciones que se obtengan también lo serán,
por muy sofisticado que sea el algoritmo que se utilice.
Las herramientas computacionales asimismo nos permiten resolver con
mayor facilidad las ecuaciones que describen a los modelos matemáticos. Nos han
mostrado el tipo de curvas que se obtienen con el modelo SIR, y esto nos
permite ajustar los parámetros de las curvas a los datos registrados en el curso
de una epidemia para predecir su comportamiento. A continuación
mostramos un ejercicio de este tipo aplicado a la pandemia actual.
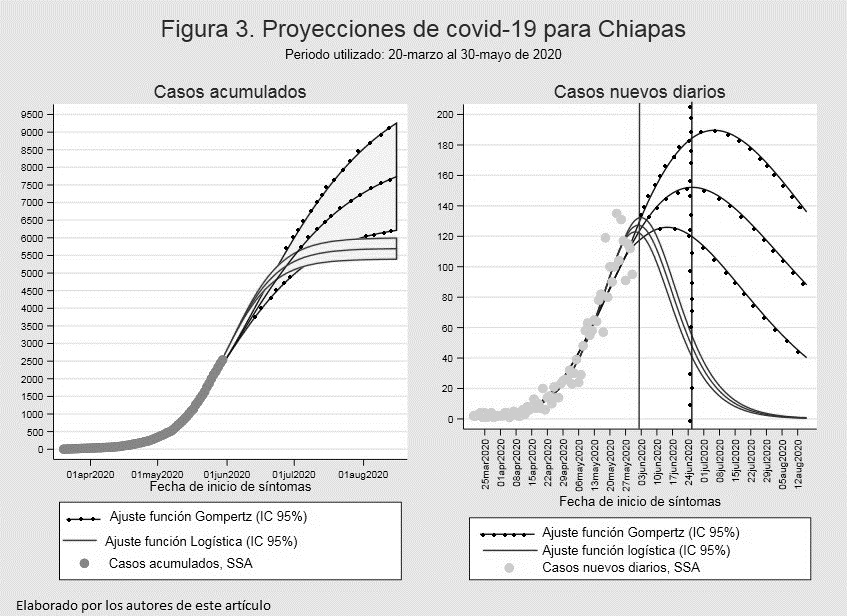
En la figura 3 se observa nuestra proyección de casos diarios acumulados y
nuevos de covid-19 para Chiapas. Utilizamos dos métodos de modelación: la
función logística, la cual se ajusta mejor a la subida de la curva epidémica, y
la función Gompertz, para la bajada y determinación del
acmé o pico máximo de contagios. Como nosotros, hay múltiples grupos de
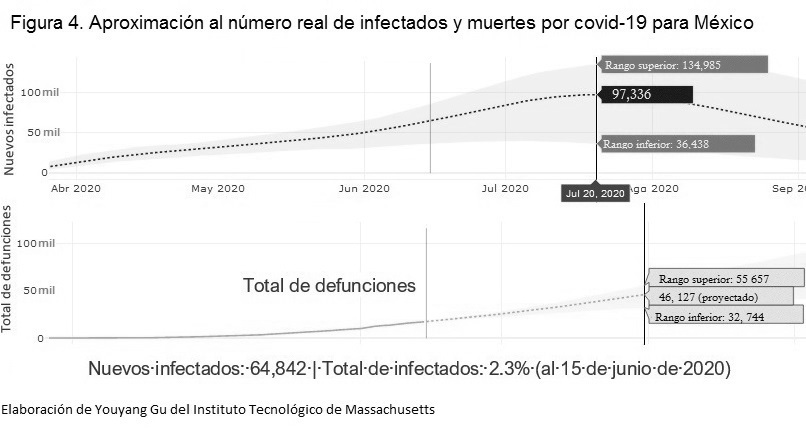
investigación en todo el mundo; por ejemplo, el del Instituto Tecnológico de
Massachusetts creó una plataforma en línea con proyecciones de infectados y
defunciones, utilizando un modelo intuitivo que estima el número real de
infectados y no solo aquellos con una prueba positiva a covid-19. Este modelo
utiliza técnicas de aprendizaje automatizado (machine learning) y se autoactualiza diariamente para Estados Unidos, sus 50
estados y para más de 70 países. Véase la figura 4 para el caso de México (https://covid19-projections.com/mexico,
consultado el 15 de junio de 2020).
En conclusión, una aplicación importante de los modelos matemáticos es
apoyar la toma de decisiones y gestión de las epidemias, principalmente para
determinar el impacto de las medidas de mitigación, identificar los grupos
vulnerables, determinar las necesidades de camas hospitalarias y otras acciones.
No hay que olvidar que se trata de abstracciones que permiten elaborar inferencias
y predicciones, pero a final de cuentas, debido a los medios de propagación del
virus, serán las personas y su comportamiento lo que definan cómo se extiende la
epidemia.
(1)
El cálculo de la esperanza de vida se basa en un modelo matemático que utiliza las
tablas de mortalidad de una población o una generación determinadas, para
estimar la expectativa de vida (en años) al nacer o a determinada edad; es un
excelente indicador del impacto que tiene una medida preventiva como las
vacunas, en este caso la de la viruela.
(2)
En los modelos compartimentales la población bajo
estudio se divide en compartimentos caracterizados por estadios relevantes de
la enfermedad, y se realizan estimaciones acerca de la naturaleza y las tasas
de transferencia entre los compartimentos.
Héctor Ochoa Díaz López
es investigador del Departamento de Salud, ECOSUR San Cristóbal (hochoa@ecosur.mx). Roberto Solís Hernández es técnico
académico del mismo departamento y unidad (rsolis@ecosur.mx). José Ocampo López Escalera es estudiante
del Doctorado en Ecología y Desarrollo Sustentable de ECOSUR (jose.ocampo@estudianteposgrado.ecosur.mx).
César Irecta Nájera es investigador del Departamento
de Salud, ECOSUR Villahermosa (cirecta@ecosur.mx).
Ecofronteras,
2020, vol. 24, núm. 70, pp. 2-5, ISSN 2007-4549 (revista impresa), E-ISSN
2448-8577 (revista digital). Licencia CC (no comercial, no obras derivadas);
notificar reproducciones a llopez@ecosur.mx